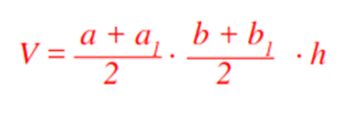BIM (Building Information Modeling)
-3- Les volumes
3.1) Les Parallélépipèdes
Les parallélépipèdes sont constitués de lignes parallèles.
Le CUBE
Formule
Le PARALLÉLÉPIPÈDE RECTANGLE
Formule
3.2) Les Prismes
Les Prismes sont des volumes constitués d'une section régulière et de longueurs égales et parallèles.
Représentation de Prismes
de section Circulaire
de section Triangulaire
de section Hexagonale
Formule du Volume
3.3) Pyramides et cônes
Les Pyramides sont des volumes constitués d'une aire de base régulière et d'un sommet sur lequel se raccorde les lignes provenant de chacun des côtés de la base
Représentation de Pyramides
à base Rectangulaire
à base Rectangulaire
à base Triangulaire
à base Hexagonale
à base Circulaire
à base Circulaire
Formule du Volume
3.4) Les autres formes
Présentation d'autres formes
La Sphère
Le Coin à base rectangulaire
Formule des Volumes
3.5) Les Volumes tronqués
La Pyramide tronquée et le cône tronqué sont des volumes simples qui ont des particularités qui méritent un développement.
3.5.1) La Pyramide tronquée
Il existe 3 formules. Les formules dites "SIMPLIFIÉES" sont utilisées fréquemment dans les métiers du bâtiment (maçonnerie, terrassement, etc...), car la précision des résultats est généralement suffisante.
Représentation
Formule simplifiée 1
Le résultat sera approximatif et inférieur au résultat juste.
Formule simplifiée 2
Le résultat sera approximatif et supérieur au résultat juste.
Formule juste
Le résultat sera juste.
3.5.2) Le cône tronqué
Représentation
Formule simplifiée
Le résultat sera approximatif et supérieur au résultat juste.
Formule juste
Le résultat sera juste.
3.5.3) Exemple de calcul
a) Bidon à mortier
Calculez le volume du bidon à mortier ci-dessous en utilisant la formule précise.
Représentation
Cotes en cm
Rappel des dimensions (cotes en cm)
Rappel de la Formule juste
Application de la Formule juste
b) Fouille de terrassement
Calculez le volume de la fouille de terrassement en pleine masse en utilisant les 3 formules (2 approximatives et 1 juste).
Représentation
Cotes en m
Rappel des dimensions (cotes en m)
-1- Veuillez noter les données du problème !
Application de la 1ère Formule approximative
-2- Veuillez écrire la 1ère formule approximative !
-3- Faites l'Application numérique !
Application de la 2nde Formule approximative
-4- Veuillez écrire la 2nde formule approximative !
-5- Faites l'Application numérique !
Application de la Formule juste
-6- Veuillez écrire la formule juste !
-7- Faites l'Application numérique !
3.6) Les Volumes composés
On trouve 2 types de volumes composés:
- Les volumes ayant une forme irrégulière, mais une épaisseur régulière;
- les volumes composés de plusieurs formes régulières.
Pour calculer le volume d'un corps dont l'épaisseur est régulière, on multiplie l'aire de la base pas l'épaisseur.
3.6.1) Exemple 1
Ce volume possède une épaisseur régulière, on peut donc calculer la surface (l'aire) de la base et la multiplier par l'épaisseur.
Représentation (cotes en m)
Résolution
-1- La base est décomposée en 2 surfaces S1 et S2, soient:
-2- La Surface totale de la base correspond à la somme des 2 surfaces S1 et S2, soit:
-3- Le Volume est obtenu en multipliant la Surface totale par l'épaisseur, soit:
Pour calculer le volume d'un corps dont l'épaisseur est régulière, on multiplie l'aire de la base pas l'épaisseur.
3.6.2) Exemple 1
Ce volume est constitué d'une pyramide et d'un parallélépipède rectangle.
Représentation (cotes en m)
Résolution
-1- Calcul du volume du Parallélépipède rectangle.
-2- Calcul de la pyramide.
-3- Addition des 2 volumes (Parallélépipède + Pyramide).
