Mécanique des fluides
1-Hydrostatique
1-1) Fluide incompressible
Les GAZ
Un fluide est une substance déformable lorsqu'elle est soumise à une force, c'est-à-dire qu'elle a la capacité de prendre la forme du contenant dans lequel elle se trouve.
On regroupe sous cette appellation les GAZ, qui sont des fluides compressibles, et les LIQUIDES, qui sont des fluides peu ou pas compressibles (incompressible).
Les LIQUIDES
Remarque: La masse volumique (ρ) d'un fluide incompressible reste CONSTANTE (ρ en kg/m3).
1-2) Pression en un point d'un Fluide incompressible
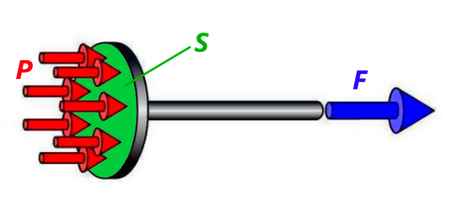
La pression P est une Force F appliquée perpendiculairement sur une Surface S.
Pour déterminer la pression p exercée sur un objet, il faut utiliser la formule suivante:
Exemple ci-contre ---->
Vérin dont la Pression P s'exerce sur la Surface S du piston, générant une Force F.
Avec:
* P représente la pression (uniformément répartie, par hypothèse d'étude, et identique dans toutes les directions) en Méga Pascal (MPa ou N/mm2).
* F représente la Force en Newtons (N)
* S représente la Surface sur laquelle la Force est appliquée en mètres carré (mm2)
Remarque:
Autre unité de pression: Le bar avec 1 bar = 105 Pascal = 0,1 N/mm2.
1-2-1) Applications
Effort de poussée
Effort de traction
Multiplicateur de pression
1-3) Équation fondamentale de l'Hydrostatique
Dans un fluide incompressible et au repos, la différence de pression Δp entre 2 points A et B du fluide est donnée par la relation:
PB − PA = ρ ⨯ g ⨯ ( ZA − ZB ) ou Δp = ρ ⨯ g ⨯ h
Avec:
- PA et PB: Pressions aux points A et B en Pascals (Pa);
- ρ: Masse volumique (densité) du fluide en kilogramme par mètre cube (kg/m3);
- g: Accélération de la pesanteur en mètres par seconde au carré (m/s2);
- ZA et ZB: Altitudes des points A et B en mètres (m);
- Δp = Différence de Pression entre 2 points (ici, |PB − PA|);
- h = Différence de hauteur en 2 points (ici, |ZA − ZB|);
Exemples de masses volumiques
La pression en B est supérieure à la pression en A
La pression est plus forte au fond de la bouteille qu'en surface
1-3-1) Applications
Château d'eau
Plongeur
Essai de laboratoire
1-3-2) Principes des Vases communicants
On utilise le principe des vases communicants pour repérer, grâce à un tube transparent relié à une cuve, la hauteur de liquide contenu dans cette cuve.
En effet, dans un même liquide, les surfaces soumises à la même pression, sont dans le même plan horizontal, puisque nous savons que la surface libre d'un liquide au repos est toujours horizontale.
La pression est donc constante dans tout plan horizontal situé à l'intérieur du liquide (surface isobare).
1-3-3) Évaluation d'une pression en hauteur de liquide
a) Réservoir fermé
Considérons un réservoir fermé contenant un liquide. Celui-ci est soumis sur sa surface à une pression ambiante Pamb.
Relions ce réservoir à un tube dont l'autre extrémité est à l'air libre !
La hauteur de liquide au dessus de la surface libre, dans le tube, permet d'évaluer la pression qui règne dans le volume libre du réservoir.
Ainsi, on a l'équation fondamentale de l'Hydrostatique, soit:
PB − PA = ρ ⨯ g ⨯ h
C'est à dire:
Pamb − Patm = ρ ⨯ g ⨯ h
Avec:
Pamb − Patm = Pe (pression effective)
Application numérique
La cuve contient du vin (densité = 0,99 kg/dm3) et on relève h = 0,6m.
L'application de l'équation fondamentale de l'Hydrostatique donne:
Pe = ρ ⨯ g ⨯ h
Pe = 990 ⨯ 9,81 ⨯ 0,6
Pe = 5827,14 Pa (5,827.10-3 MPa = 5,827.10-3 N/mm² = 58,27.10-3 bar)
Soit une pression effective:
Pe = 0,058 bar
b) Tube retourné sur bâche
Considérons la manipulation suivante (voir représentation ci-contre):
Retournons un tube plein de liquide sur sa bâche. Le liquide descend dans le tube retourné en créant un vide absolu et se stabilise à la hauteur h.
Entre A et B, on peut écrire en appliquant l'Équation fondamentale de l'Hydrostatique:
PB − PA = ρ ⨯ g ⨯ h
Résultats
1-4) Théorème de Pascal
a) Énoncé & Définition
Dans un fluide incompressible au repos, toute variation de pression en un point A engendre la même variation en tous points B du fluide.
b) Application
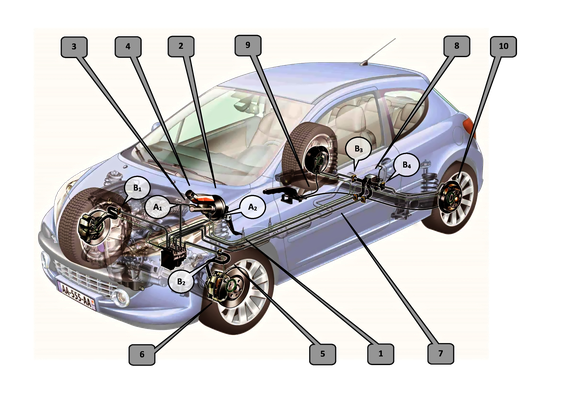
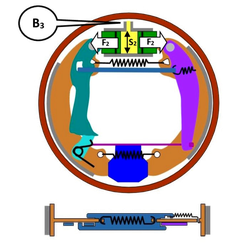
Soit le véhicule automobile ci-contre et son circuit de freinage constitué de:
- Un maître cylindre (3);
- Des cylindres de roue (6) et (10), respectivement:
--> (6) Cylindre d'étrier = piston;
--> (10) Cylindre de frein tambour.
Des canalisations les relient et un réservoir assure un remplissage exempt de poches d'air.
c) Description & Analyse
* "Mastervac"
Le principe "Mastervac" permet d'obtenir un freinage assisté:
Un effort modéré sur la pédale de frein (1) se traduit par un effort plus important sur le piston du maître cylindre (3).
* "Maitre cylindre tandem"
Le "Maitre cylindre tandem" (3) permet de séparer le système de freinage en deux circuits indépendants. En cas d'incident sur l'un des circuits, l'autre reste actif.
Circuit de freinage d'une automobile
Légende
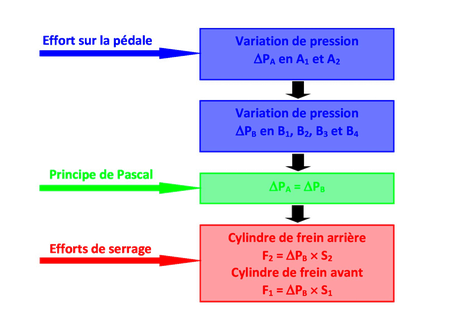
* Principe de Pascal (modélisation ci-dessous)
L'application d'un Effort supplémentaire ΔF sur la pédale de frein engendre une augmentation ΔPA de la pression aux sorties A1 et A2.
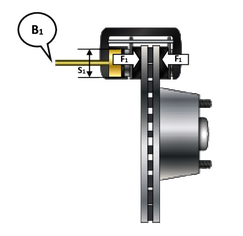
Il en résulte des variations de pression ΔPB aux points B1, B2, B3 et B4 proches des cylindres de freins.
Principe de Pascal
Étrier avant
Tambour arrière
1-5) Théorème d'Archimède
Tout corps plongé dans un Liquide (L) reçoit de ce Liquide (L) une Force hydrostatique (Fl) de bas en haut, égale au poids du volume de liquide déplacé.
Cette Force (ou Poussée) ne dépend pas de la nature du Corps flottant (S).
Fl = ρ ⨯ g ⨯ V
Avec:
---> ρ = masse volumique du Liquide (L) en kg/m3;
---> g = accélération de la pesanteur en m/s2;
---> V = Volume du Liquide (L) déplacé en m3.
1-5-1) Application
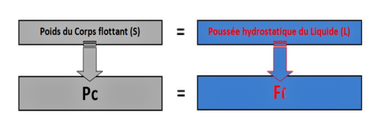
Soit un Corps (S) de poids (Pc) flottant sur un Liquide(L).
Le Corps flottant (S) reçoit du Liquide (L) des forces fl (agissant perpendiculairement et uniformément, par hypothèses d'étude).
Ces mêmes forces fl agissent sur la forme (S') de Liquide (L)
COURS EN CONSTRUCTION !!!
